FX Pass Through
I will analyze to examine the myth of EM FX pass-through. Below you can see the definition of FX pass through from Ashmore's Article:
Background and Theory
One of the common perceptions about emerging markets (EMs) is that inflation rises sharply when currencies weaken, because weaker currencies push up domestic prices of imported goods and services. This phenomenon has a name: FX pass-through.
As the previous sentence is directly quoted from the Ashmore's article linked above, the phenomenon is generally formulated with the following regression formula:
\[\Delta ln(p_t) = \alpha + \sum_{i=0}^{N}\Delta e_{t-1} + \delta\Delta ln(c_t) +\psi \Delta ln(d_t) +\epsilon_t \]
where
- p is import price,
- e is the exchange rate
- c is marginal costs
- d is demand
- \(\Delta\) sign denotes the difference.
If you are interested in the subject and want an academic level analysis of the phenomenon. Here, you can find this paper from Bank of Canada, examining exchange rate pass-through due to the depreciation of Canadian Dollar against US Dollar in previous years, useful.
Data
I am planning to use monthly data from 2005 to 2017 on Turkish Lira against US Dollar (USDTRY) and Consumer Price Index.
Quandl enables us to reach these public data in CSV format.
The Foreign Exchange Rate (USDTRY) data is from Bank of England available on Quandle.
The CPI inflation data is from Central Bank of Turkish Republic available on Quandle.
Objectives
- Does FX rate depreciation have an effect on consumer prices?
- If there is an effect, what is the mean FxPassThrough value for the depreciation periods?
Hypothesis
I believe FX rate depreciation has a positive effect on consumer prices for the depreciation periods. I will try to see what is the level for Turkey in the period between 2005 and 2017 when Turkish Lira depreciated against US Dollars.
Analysis
I used tried linear regression model to see the association between foreign exchange pass through and consumer price inflation. I performed linear model in both for all periods and for only periods TRY has depreciated against USD.
Running the Analysis
Clone the repo and follow the instructions on FXPassThrough Project Repository. This project is an automated by makefile, you can run and produce the same results by following the instructions.
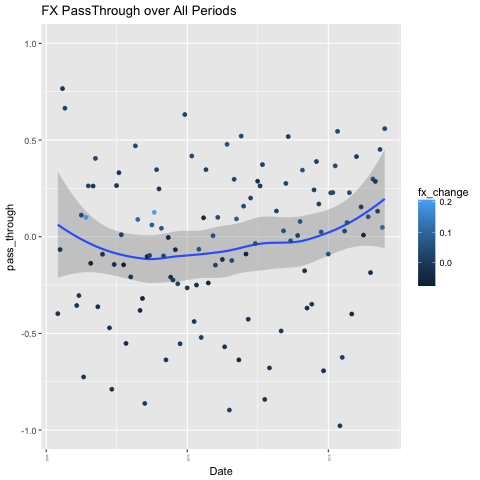
Exhange Rate Pass-through in Turkey over time(2005-2017):
I will use the model below which is also used in Pimco's report:
\[cpi_{t} = \beta_0 + \beta_{1}* FXrate_{t-1} + \beta_{2}* FXrate_{t} + \beta_{3}* FXrate_{t-1}+\epsilon\]
which is our first model.
The regression result on general data shows us the change in the exchange rate in both t-1 and t do not have a significant affect on consumer price inflation. In this data, we cannot find enough evidence to believe any relationship between exchange rate and consumer price index.
However, our hypothesis is if the exchange rate shocks have any affect on the consumer price index. Therefore we should use the following regression for the periods where fx_change is bigger than zero which means where Turkish Lira depreciated against US Dollars.
\[cpi_{t} = \beta_0 + \beta_{1}* + \beta_{2}* fxchange_{t} +\epsilon\]
\[fxchange = \frac{FXrate_{t}}{FXrate_{t-1}}-1\]
Here, you can see the trend for depreciation periods:
This graph confirms the 0.046 at the linear model result for fx_change onto cpi. We can say pass_through will be around 0.5 for depreciation period which makes sense as we define pass_through as cpi/fx_change.
This is the second linear model results above, and it gives a significant result for FX change. It means we have enough evidence to believe "FX losses has affect on the local currency TRY" to depreciate against a major currency such as USD.
It is a very primitive analysis to see the affect of foreign exchange losses on a developing countries consumer price index. But, luckily we have a significant result to encourage us for further analyses.
Future Analyses
For the future analysis, it can be better to examine the inflation spread with the US would be better variable since we can eliminate the US inflation effect on the exchange rate.
Another assignment would be to use a more complicated model like the one shown in the introduction.