Explanation of Hypothesis Testing, Type I and Type II Errors with Examples:

Let’s think you were at a bar and drinking your beer with your friends. Some drunk guys started fighting next to you, and you tried to stop them. One man shot another and left the gun in your pocket. Then, the police were there, got you and some of the guys. But, the guy fired the gun had found a way to escape. They took you all into custody to reveal who shot that poor man. In the end, you have been found guilty, and nobody even talked about the guy escaped.

Is it fair? No, it does not seem fair to put you in jail and let the real offender escape.

This mistake comes up due to the nature of decision-making. How and, more importantly, why?

To get to that point, I need to explain what hypothesis testing is. First of all, what is hypothesis testing?

It is a statistical way of verification of a claim, and it is called the hypothesis testing. At hypothesis testing, your question has two alternative answers either “You are guilty.", or “You are not guilty.".

You pick one of those as your basis without knowing if it is true or not. What you choose is called the null hypothesis. The other one is called the alternative hypothesis.

Let’s say we choose “You are guilty” as our null hypothesis. As I said before, it doesn’t matter if it is true or false at this stage.

Then, it is good to list what all possible values of this case are. The hypothesis test can give four possible results for this question.

1. Although you are not guilty, the judge declares you are guilty. False!
2. You are not guilty, and the judge declares you are not guilty. True!
3. You are guilty, and the judge declares you are guilty. True!
4. You are guilty, but the judge declares you are not guilty. False!

The judge makes a wrong decision in the 2nd and 4th. In statistics, these two cases have different meanings.

For 2nd case, although you are not guilty, you are sent to the jail. This is the incorrect rejection of a true null hypothesis; it represents a “False Positive” called the “Type I Error”.

For 4th case, think the question, again, “Is the guy escaped guilty?" Yes, but they let him free. It is an example of incorrectly retaining a false null hypothesis. It represents a “False Negative” called the “Type II Error”.

Both errors work against each other. When you make an analysis, you will always have the error. Therefore, you need to trade off between two. The graph below visualizes how the errors overlap.

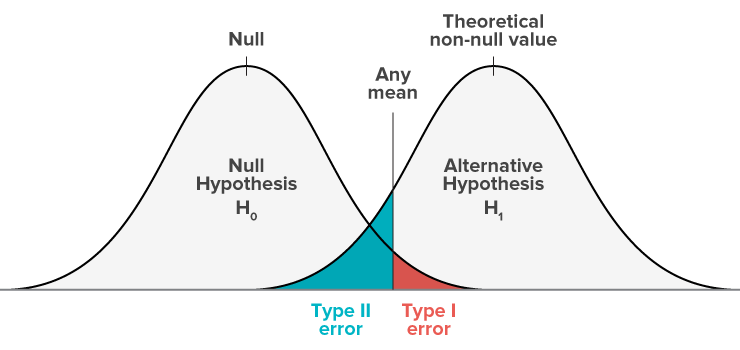
Image source: http://math.emory.edu/~lchen41/teaching/2020_Spring/Chapter-6_compact.pdf

You want to catch all criminals. At the same time, you care human rights as the law says one is “innocent until proven guilty”. But, in real life, you have to sacrifice one or the other.

As human rights are essential, you may have to release some criminals due to the insufficiency of evidence. In this case, your primary goal is minimizing the “false positives”(type I error). You want to catch all the criminals but have to be careful with human rights, and be sure with enough evidence.

We can touch on another example to grasp the concept better. In this case, you feel under the weather and go to a medical examination. You tell the doctor how you fell and the doctor makes some tests and diagnoses what your situation is.

Now, it is time to apply what we learn from the previous example. First of all, we need a null hypothesis. Assume, our null hypothesis is “You have a disease.". Then, we can make a table to summarize what all cases are.

	You are sick (Null Hypothesis)	You are not sick (Alternative Hypothesis)
The doctor says you have a disease	Right Decision!	False Positive (Type I Error)
The doctor says you don’t have a disease	False Negative (Type II Error)	Right Decision!

Imagine that the doctor says you are alright although you have a disease. Then, your disease may lead serious issues.

On the other hand, the doctor may prescribe medication although you are alright. You take that medication which may have serious side-effects.

In both cases, the doctor unintentionally makes a mistake, and it affects your life severely. Now, think which one you prefer, the doctor either prescribes unnecessary medication or leaves you untreated you when you need treatment.

It may be the reason some doctors tend to prescribe medication to keep them safe, and they may think side-effects are small issues compared to the illnesses. Here, the doctor intuitively tries to minimize “false negatives”(type II error).

As you realize, for our examples, the judge and the doctor tend to minimize different types of errors.

All in all, one should be careful while doing an analysis and decide which error is more dangerous for his/her study. So, as data scientists, we need to select accuracy measures derived from confusion matrix carefully.